MATRICE, VEKTORI I RAČUNSKE OPERACIJE

Kako je već rečeno, osnovni objekt u Matlabu je matrica, tj. pravokutna tablica brojeva koja se izravno zadaje kao niz brojeva u uglatim zagradama. Pri tom se retci razdvajaju točka-zarezom, a elementi unutar retka bjelinom (ili zarezom). Npr: 

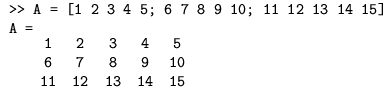
zadaje matricu reda 3 × 5 od 3 retka i 5 stupaca, koja bi se u matematici pisala s: 

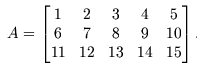
Snaga Matlaba nalazi se u velikim mogućnostima manipulacije matricama. Npr.: 

• Izgradnja novih matrica izvlačenjem elemenata iz postojećih: Element iz drugog retka i trećeg stupca je skalar, tj. matrica reda 1 × 1: 

   

  

   

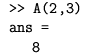
  Elementi iz drugog retka, te petog i trećeg stupca čine redak-vektor, tj. matricu reda 1 × 2: 

   

  

   

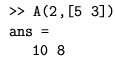
  Podmatrica sačinjena iz elemenata u presjeku prvog i drugog retka, te trećeg i četvrtog stupca je reda 2 × 2: 

   

  

   

• Transponiranje: 

   

   

   

• Lijepljenje (konkatenacija) matrica i vektora se vrši na intuitivan način (kako to zamišlja mali Ivica): 

   

  

   

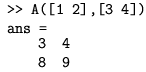
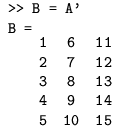
Vidimo da znak  ";"  znači "stavi ispod", a bjelina "stavi pored". Pokušajte isto napraviti u Fortranu. Ukoliko dimezije matrica ne omogućavaju matematički ispravno slaganje, Matlab će javiti pogrešku: 

 



 

Primijetimo internu varijablu ans. Ona uvijek sadrži rezultat zadnje izvršene operacije i može se ravnopravno koristiti u sljedećoj operaciji. Ako se rezultat ne imenuje izravno, ispisuje se preko varijable ans.

• Operator dvotočke ":" jedan je od najčešće korištenih. Njime se zadaje 
  raspon indeksa: 

   

  

   

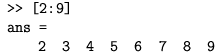
  Malo općenitiji oblik je:

   

   

   

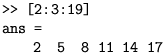
  u kojem srednji broj ima značenje koraka. Slijede primjeri s indeksiranjem redaka i stupaca matrica. 

   

  

   

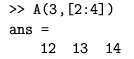
  tj. izvlače se elementi iz trećeg retka, te drugog do četvrtog stupca. Isto se može zadati s 

   

   

   

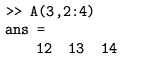
  Ako se stavi samo dvotočka, tj. 

   

  

   

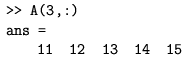
  dobiju se svi (u ovom slučaju) stupci. Izraz A(:,:) isto je što i A. No A(:) daje vektor-stupac koji se sastoji od stupaca matrice A i koji u našem primjeru ima 15 elemenata. Inače elemente (2-dimenzionalne) matrice je moguće osim pomoću dvostrukog, dohvatiti i korištenjem jednostrukog indeksa koji napreduje odozgo prema dolje i s lijeva u desno po stupcima. Na primjer:

   

  

   

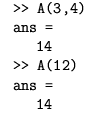
  Osim što ukazuje na fortransko porijeklo i na prvi pogled djeluje kao "komplikacija", dualnost u indeksiranju je vrlo korisna i jedan je od primjera promišljenosti Matlaba.

  Unutar pojedine matrice moguće je indeks zadnjeg retka ili stupca zamijeniti varijablom end. Npr. 

   

  

   

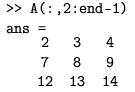
  čime smo izvukli sve retke matrice A, te stupce od drugog do pretposljednjeg. Uočimo da nije potrebno pamtiti koliko stupaca ima matrica A. To za nas radi Matlab. 

• Matlab, kako smo već rekli, ne zahtijeva izravno deklariranje varijabli. štoviše, varijable tijekom rada, osim vrijednosti, mogu mijenjati i veličinu i tip. Ovo je posve protivno Fortranu i od korisnika s fortranskim iskustvom zahtijeva izvjesnu prilagodbu u načinu razmišljanja. Na primjer, ako se zahvati element matrice izvan najvećeg retka ili stupca, Matlab će automatski matricu redimenzionirati, te napuniti nulama odgovarajuće elemente. 

   

  

   

  Ipak, matricu koja će se računati postepeno u petlji, dobro je na početku zadati u konačnoj veličini. Time se izbjegava stalno redimenzioniranje i značajno ubrzava račun. Želimo li sve brojeve u postojećoj matrici (npr. c zamijeniti jednim te istim brojem (npr. 7), nije dobro napisati c = 7. Time bi postojeću matricu c (ovdje reda 5 × 4) zamijenili skalarom 7 (tj. matricom reda 1 × 1). Umjesto toga treba koristiti: 

   

  

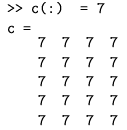
Navedimo još neke, vrlo korisne funkcije za rad s matricama: 

• size(A)
  za matricu A reda m ×  n vraća vektor [m n] njenih dimenzija. 
• length(A) 
  vraća veću od dvije dimenzije matrice A. 
• repmat(A,m,n) 
  je matrica dobivena tako da se svaki element matrice od m redaka i n stupaca zamijeni matricom A. Na primjer 

   

  

  

   

• zeros(m,n) daje isto što i repmat(0,m,n). 

   

  

   

• ones(m,n) daje isto što i repmat(1,m,n). 

   

   

   

• A1 = reshape(A,m1,n1) je iznimno upotrebljiva funkcija koja gradi matricu preslagivanjem po stupcima zadane, postojeće matrice. Naime, elementi matrice A se iscrpuljuju po stupcima i njima se puni matrica A1, također po stupcima. Pri tom je A1 reda m1 × n1, a ukupan broj elemenata mora ostati nepromijenjen. 

   

  

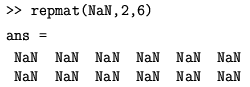
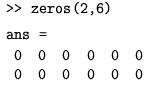
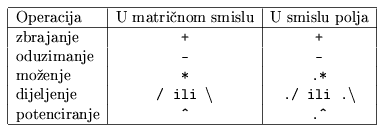
Osnovne računske operacije prirodno se vrše nad matricama i vektorima. Pri tom razlikujemo operacije koje se vrše prema pravilima matrične algebre (kratko "u matričnom smislu"), te operacije koje se vrše po elementima (kratko "u smislu polja", engl. array). Oznake su sljedeće

Zbrajanje (oduzimanje) u matričnom smislu, istovjetno je zbrajanju (oduzimanju) po elementima. 

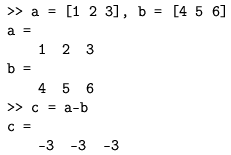
Množenje u matričnom smislu je definirano ako se broj stupaca prev matrice podudara s brojem redaka druge matrice: 

Matrično dijeljenje zapravo znači množenje s inverznom matricom, odnosno rješavanje sustava linearnih jednadžbi. Obzirom da množenje matrica, za razliku od skalara nije komutativno, razlikujemo moženje inverznom matricom s lijeva i s desna. 

Potenciranje u smislu matrica je definirano za kvadratne matrice.

Operacije u smislu polja, definirane su na prirodan način za operande (matrice) istog reda, ili ako je jedna od njih skalar. Na primjer: 

rezultira greškom, budući da matrica a nije kvadratna.

U Matlab su kao interne ugrađene sve elementarne, te mnoge specijalne matematičke funkcije. Sve su definirane u punoj matematičkoj općenitosti u kompleksnoj ravnini, a primjenjene na matricu djeluju po elementima. Npr.