
VALOVI U ROTIRAJUĆEM FLUIDU
Činjenica da je Zemlja elipsoid koji rotira oko svoje osi uvjetuje da na česticu, koja gibanjem mijenja svoju geografsku širinu, djeluje i tzv. Coriolisova sila. Coriolisova sila nastaje zbog rotiranja sustava Zemlje u odnosu na referentni sustav. Posljedica jest zakretanje čestica udesno na sjevernoj Zemljinoj polutci, te ulijevo na južnoj Zemljinoj polutci.
Posljedica rotacije Zemlje jest i sačuvanje potencijalne vrtložnosti u moru i atmosferi. Potencijalna vrtložnost se definira kao
![]()
gdje je f Coriolisov parametar, ζ relativna vrtložnost te h dubina mora.
Jedna od posljedica sačuvanja potencijalne vrtložnosti u moru i u atmosferi jest postojanje planetarnih ili Rossbyjevih valova. Mogu biti barotropni ili baroklini, a smjer gibanja im je uvijek od istoka prema zapadu. Brzina njihovog gibanja je definirana izrazom
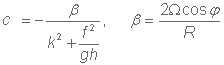
gdje je k valni broj, R radijus Zemlje, φ geografska širina te Ω kutna brzina rotacije Zemlje. Iz relacije je vidljivo da su Rossbyjevi valovi disperzivni.
Dakle, kada česticu pomaknemo uzduž meridijana, ona biva vraćena nazad zbog sačuvanja potencijalne vrtložnosti. Pri tome, cijeli sustav se giba prema zapadu te na taj način zonski transportira energiju u moru. Valna duljina Rossbyjevih valova iznosi više stotina kilometara, dok im je brzina mala, do 10 cm/s, te putovanje valova i transport energije preko oceana može trajati mjesecima pa čak i godinama. Pri tome vrijedi geostrofička aproksimacija.
Važnost Rossbyjevih valova jest u prijenosu energije na velike udaljenosti u oceanima, pojačavanje i slabljenje stalnih strujnih sustava u oceanima, djelovanje na prostorno-vremenske razdiobe termohalinih i drugih svojstava mora, procese na površini mora te u konačnici na klimatske karakteristike pojedinih područja.
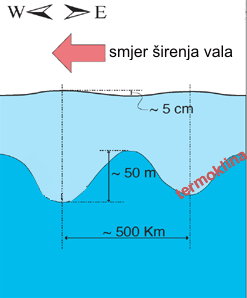
Shematski prikaz Rossbyjevog vala u moru.
Druga skupina valova u rotirajućem fluidu su težinsko-inercijalni valovi. Ova skupina valova ima period blizu inercijskog perioda (inercijski period se definira kao 2π/f ). Disperzijska relacija je definirana kao
![]()
prema tome valovi su nedisperzijski u slučaju kada je sila teža dominirajuća
(gh
>> f2/k2), dok su disperzijski ako je Coriolisova sila relaksirajuća
(gh
<< f2/k2). U prvom slučaju riječ je o težinskim
valovima, a njihov poseban slučaj su
slobodne oscilacije - seši, dok je potonji uvjet karakterističan za barotropne
inercijske oscilacije, kao i za topografski uvjetovane Kelvinove valove. Karakteristika
inercijskih oscilacija je kruženje strujnog polja u nekom području, koje obično nastaje kao rezultat djelovanja vjetra na površinu mora.
Veličina koja opisuje omjere djelovanja sile teže i Coriolisove sile na valne poremećaje u moru naziva se Rossbyjev radijus deformacije a i definira se kao
![]()
Ako uvrstimo vrijednosti karakteristične za oceane i umjerene geografske širine (h = 4000 m, f = 10-4 s-1), barotropni Rossbyjev radijus deformacije iznosi oko 2000 km. No, obzirom da su duboka mora stalno vertikalno stratificirana, umjesto barotropnog Rossbyjevog radijusa deformacije uvodi se baroklini Rossbyjev radijus deformacije, koji opisuje poremećaje na granici između slojeva mora. On iznosi obično od 10 do 100 km, te je stoga područje u kojima se mogu javiti unutarnje inercijalne oscilacije prošireno na veći dio svjetskih oceana i okrajnjih mora. Unutarnje inercijske oscilacije se javljaju i u Jadranu s periodom od oko 17 h, a generirane su vjetrom na površini mora.
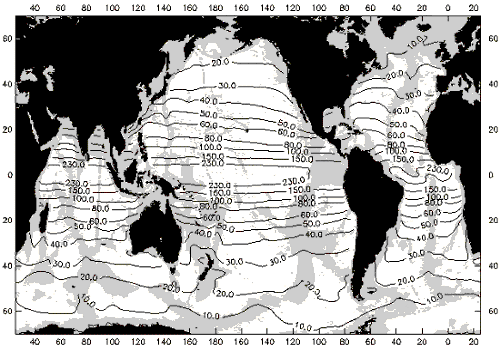
Baroklini Rossbyjev radijus deformacije u oceanima (u km).
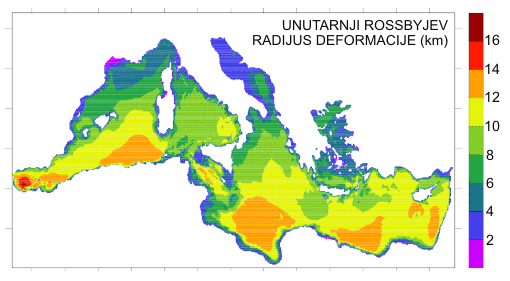
Baroklini Rossbyjev radijus deformacije (u km) u Mediteranu, izračunat za proljetno razdoblje.
Vezane stranice projekta